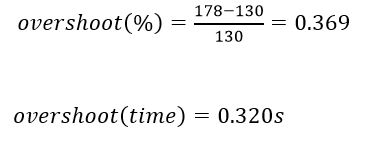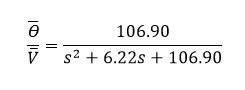Table of Contents
Ball and Beam Modelling using PID Control
We can analyze the whole system into two distinct transfer functions , one for the ball and beam , and one for the motor. After , we can analyze the whole system putting these two transfer functions together in a block diagram.
Ball and Beam Transfer Function Derivation

Analyzing the equilibrium we have:
Motor Transfer Function Derivation
One easy way to get the motor's transfer function is to plot and analyze its response to an input , and by a graphical analysis get the parameters to derive its transfer function. We can program an algorithm to read and save ( using file saving functions ) the motor position during its operation. The following code was used to save and after plot the motor response until it get to the desired angle.The code makes the motor runs from 0 to 130 degrees, controlled by PID using the function “ PosRegEnable ” .
Save this Into the same folder of your code. and include it as shown in the code.
Plotting the results we have:
By the graphic response , we can assume the motor system as a second order system (because of the oscillatory and overshoot response). As known , a second order is characterized by two parameters , natural frequency (σ) and damping ratio (ξ).We can get these parameters by the following steps:
We know that a second order transfer function is:
So the motor's transfer function is:
Motor system modeling on Simulink
We can simulate the motor system on Simulink and compare the result to the experimental result , to verify if the derivation is correct.
Comparing both responses we can see that the derivation was correct.
SIMULATING THE WHOLE SYSTEM WITH PID CONTROL
We can simulate the whole system using the ball and beam together with the motor's transfer functions to simulate the real system. We can apply the PID control as well using Simulink. The block diagram and some results are shown bellow.
Simulation a disturbance on the system ( ball goes to 30 mm ) , we can see how the system will react in order to make the final ball position 0 mm.
Using only proportional control ( system is unstable ).
Just to ilustrate that the system can be controlled using PD control, with Kp=3 and Kd=3 .We have 17,5 seconds to reject a 120 mm disturbance ( moving the ball 120mm from the center of the beam)
Working Video / Simulating Disturbance
On the video ,was simulated first a heavy disturbance , and then two small disturbances.
Comparison Simulink vs Real System
Introducing the a file saving function , the ball position over the time can be saved to a file and then plotted using an excel spreadsheet. Using KP= 1 and KI=0 and KD=0.76 and the disturbance shifting the ball to 176mm away from the setpoint.
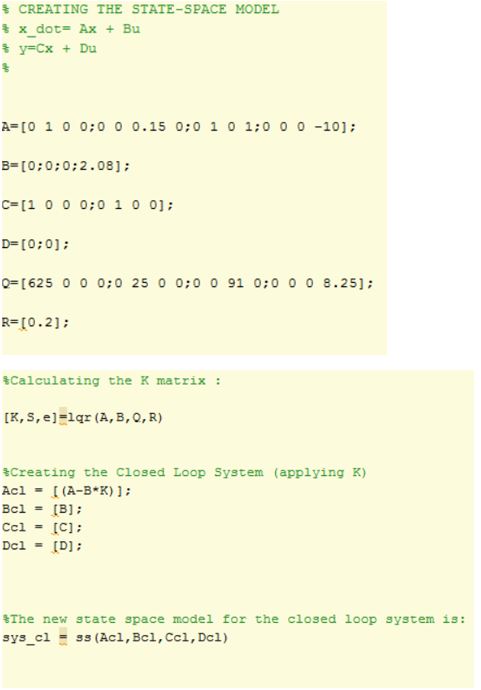
Control using LQR
PID VS LQR
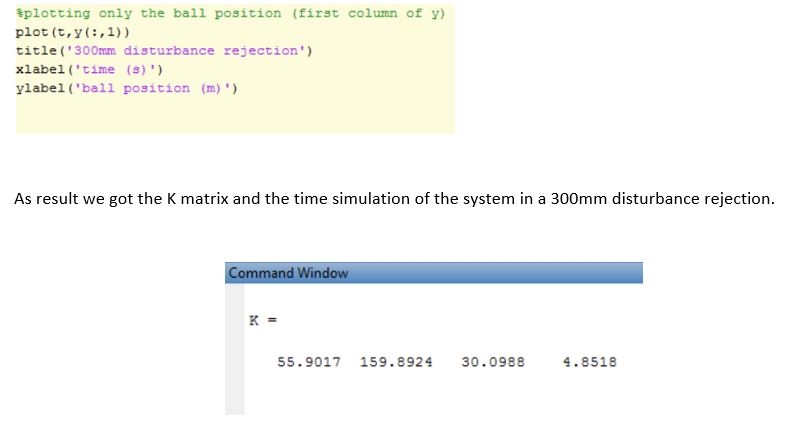
Analyzing a 176mm disturbance rejection , we have (PID first LQR second):
*note here that both methods can show pretty similar results , hand-tuning the gains after the initial guess. The PID version of the controler was intended to stop the ball fast , the LQR version of the controller was intended to stop the ball without overshooting too much. Again , both methods can be adjusted to control the overshoot or the rise time.
It's difficult to make a comparison between the PID and LQR control methods on this ball and beam case , both can be adjusted by hand after the initial guess and can show satisfactory results.However , the main advantage of using LQR on this case is that the energy input can be controlled (at the [R] matrix ). Both methods requires a hand tuning after the initial guess to achieve the desired response.
Usually you will want to use Full State feedback using LQR insted of PID - PID can be limited in some situations. On the Rotary Inverted Pendulum for example , using only PID Control is not enough to get a good pendulum balance.